Welcome! This is a "detail" page about a book purchased as part of a job lot at an auction of general household "stuff". There is an overview of the job lot, if you haven't already seen that. This is about "book h" in that overview.
Forgive me for the moment any overlap between this page and the main page...
Book "h": My notes on this are incomplete at this point.
Surveying Improved is said to be in four parts. Not only are things I expected to find covered, but there are log and trig tables... no calculators for that in those days, and Mr. Babbage's machine hadn't yet been invented to generate the tables accurately. (Of course even though he "invented" it, it didn't get built until electronic calculators were already available.)
I've barely scratched the surface of Hume's contribution so far... but I will give you the whole title: "Geodoesia Accurata: Or, Surveying made Easy by the Chain only".
Soem time ago, I asked "What, please, do you make of the letters Kennedy has put after his name?" (Click here to get my contact details to answer.)
One of the pleasures of collecting books and maps is that there are some very nice people out there, with your interests.
One of them kindly got in touch with the following suggestions, observations...
First note how neaty the "James" of the ownership inscription has been placed on the page. Now look at the "Kennedy". Looks a bit "squashed up", don't you think? And if you look closely at what follows the "Kennedy", although it seems to be similar ink, itw was not written with the care, and perhaps not with the same nib, as the "Kennedy". AND: If it was there before the "Kennedy", that would explain the squashing, wouldn't it?
It turns out that for a time, it was not uncommon for booksellers, or indeed owners, to put the cost of a book, sometimes in code (Read "Silk and Cyanide, Leo Marks, for a variety of reasons) on the title page. Booksellers today often put that kind of thing on the inside of the front board, or on the first page in the book... but go back a ways, and the binding of a book wasn't the more or less permanent feature that it is on a modern, or recently re-bound, book. Hence the title page made a better place to put such things, much as that might distress either Mr. Kennedy, who clearly liked to work neatly, or me, who prefers things "unsullied", "as they were". (I do forgive author's inscribing their books, though! And neat gift inscriptions, someplace suitable, can be okay. I was once offered a Florence Nightingale, inscribed to a much loved neice. And just missed a Milne, with Christopher Milne in a child's hand... although I gather he was sat down in front of a pile one day, and such inscriptions don't necessarily indicate that the copy in question was his copy....)
Ah! Books and maps! Their own "Never ending stories...." To get back to the Wilson/ Hume...
Here's the top half of one of the diagram plates....
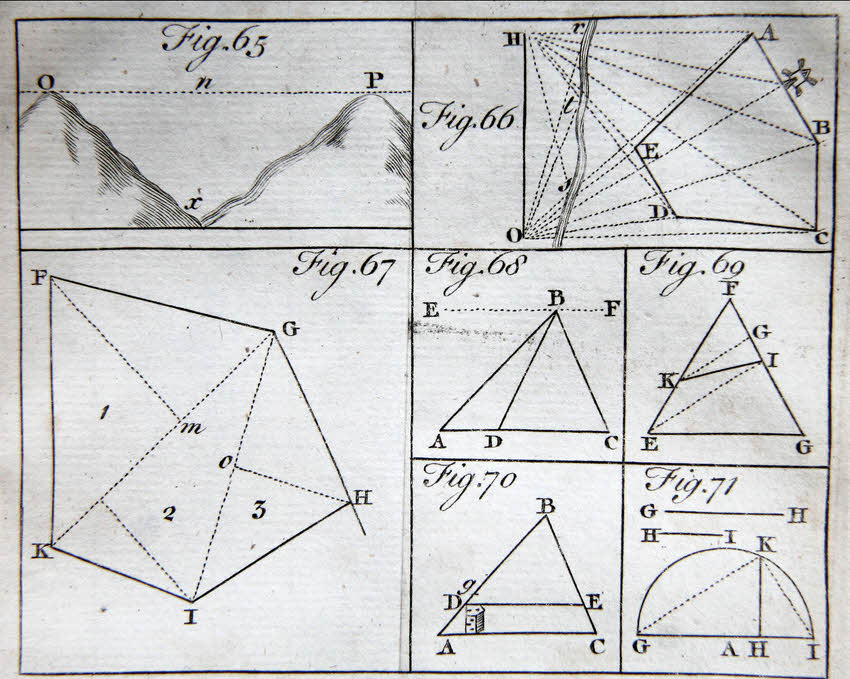
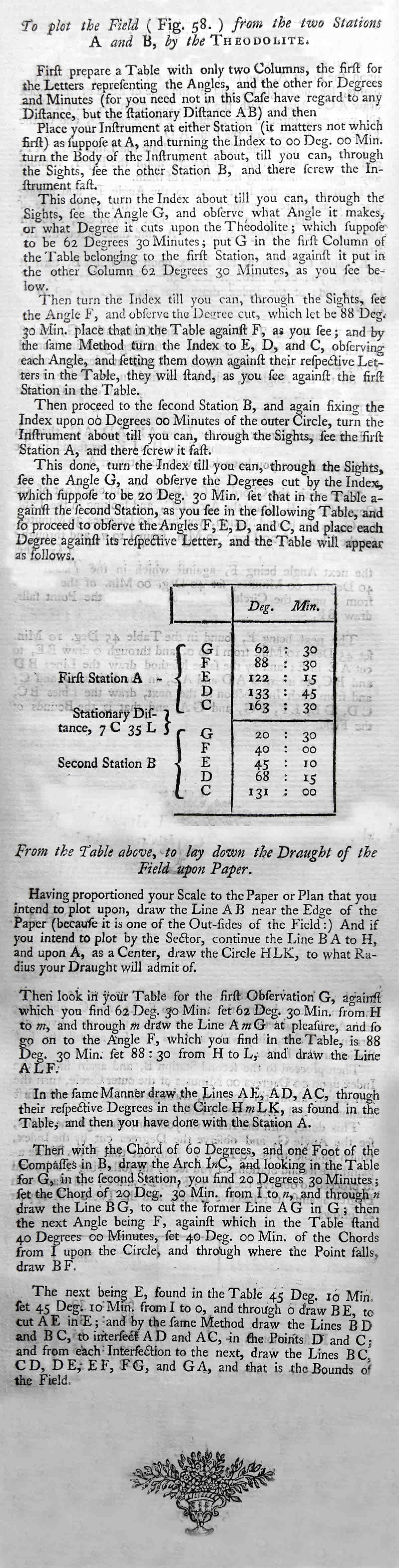
Figure 58 in the following goes with the text which follows. It is a basic exposition of mapping by triangulation, a tremendously important basic skill, used extensively for making the world's maps down the years before satellite mapping. For another guide to that, I recommend the hobbyist approach to map making explained on a retired teacher's page.
It might well be helpful to open a copy of the above in a separate window. (And re-size the result.) (The link may not work in every browser, but it will work with Firefox, at least.)
Below the image of the text from the book, there is a brief note about drawing angles by using chords, and about the matter of "where is zero".
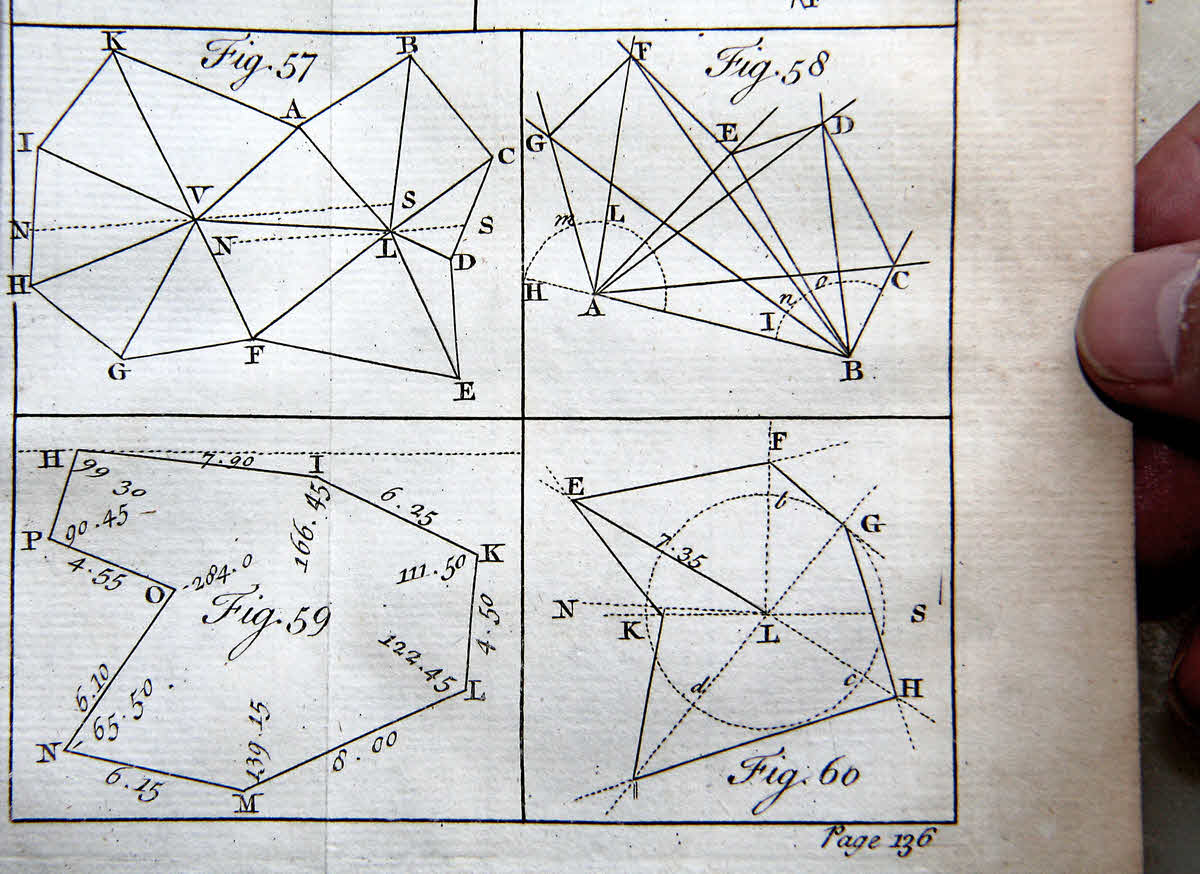
There are two things in the above which strike me as perhaps perplexing to someone unfamiliar with what the book is trying to explain.
First, "where is zero"?
To me, if I were standing at "A", I would "see" the "angle to G" as about 120 degrees. And yet, above, we are told that "the angle to G" is 60 degrees. This arises because the author of the text above is measuring HAG, not GAB. There is some sense in that approach. It seems that the author is recommending always reading your angles in a clockwise direction. This is easy for the sightings from B... ABG being 20 degrees, ABF being 40, and so on. But for the sightings from A, we just establish the line AH, and measure our angles from that. (AH being a continuation of BA). Strange at first, maybe... but there's a method in that madness.
Second: Drawing angles of a particular size by using chords. You need to draw angles to make your map from the angles measured in the field. However, for drawing angles, I would simply use a protractor! But here's an explanation of drawing them "by chords", just to show that Mr Harris's map creation method does work....
The text tells you to "draw the Circle HLK", and "draw the Arch InC". (It might have been better to say "Arch" instead of "Circle", in respect of HLK, especially as the more correct term was used in respect of Arch InC. By "Arch", he merely means what we would call an arc.)
One can infer that the author meant us to use HLK and chords to draw AG, AF, AE, AD, AC... pity he left that to our imaginations!
When he speaks of using chords to draw arcs, he leaves out some things we need to know. (They were possibly covered earlier in the book.)
If you don't have a protractor, but do have a suitable table of numbers, you can draw angle HAG as follows....
The radius of arc HmL is important. You draw an arc with a radius that is covered in the tables you have. I'm going to pretend that I have a table of numbers associated with a 5cm arc.
If I had a 5cm arc, and the right table, I could look up in my table and see that the chord (Hm) for a 60 degree angle (HAm) would be 5cm if the radius of the arc were 5cm. That is, the straight line distance from H to m would be 5cm. We also know that m is somewhere on the arc HAm. Thus, we set a pair of compasses to 5cm, put the point on H, and use the compass to mark m on HmL. Once we have m, we can draw Am. (I don't know what's wrong with using a protractor, though! Using chords does make it possible to simulate using a very large protractor, which would allow the draftsman to be more precise.)
That's the detail on this book. If you enjoyed it, you may want to go "up" to the page about the "job lot" of books it came from, at an ordinary "furniture/ jewelry/ art" auction with only about 5 lots of books out of about 350.
Editor's email address for comments or questions.
Page tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes. There were two "unknown attributes" in Google+ button code. Sigh.
....... P a g e . . . E n d s .....